في الجزء الأول, رأينا كيف أن ثقتنا في الحواسيب قد تكون في غير محلها, و أن الحواسيب قد تقوم بتصرفات غير متوقعة و تؤدي لعواقب سيئة. إن حاولنا تلخيص سبب جامع للتصرفات الغير متوقعة من الحواسيب سنواجه مشكلة – التصرفات الغير متوقعة تشمل نواحٍ متعددة و تظهر بأشكال مختلفة (كما رأينا في أمثلة الجزء الأول التي تضم مجالات و مشاكل مختلفة من حساسات الطائرات إلى نماذج تعلم الآلة). في نهاية الأمر, هذه مشاكل “غير متوقعة”, فكيف يمكن تلخيص أسبابها؟
مشكلة تلخيص السبب يجب أن لا تمنعنا من المحاولة و ذلك أن تشخيص المشكلة هو أول خطوة لحلها. و حل يشمل جميع التصرفات الغير متوقعة من الحواسيب هو طريق مغرٍ, لأن البديل هو حلول متخصصة لكل مشكلة على حدى, مما يعني أن حل أحد المشاكل لن يؤثر أو ينفع لحل المشاكل الأخرى. فإن وجدنا حلا متخصصا لمشكلة نماذج تعلم الآلة من التدوينة السابقة, لن يؤثر هذا الحل على مشكلة حساسات الطائرات. و عالم الحاسب الموجود بداخلنا (المغرم بالتجريد abstraction) سيعجبه بالتأكيد حل المشاكل المختلفة سوية!
عودة إلى محاولة تلخيص المشكلة, يبدو أن الخاصية التي تجمع بين التصرفات الغير متوقعة للحواسيب هي أنها نتجت عن طريق أخطاء برمجية أدت إما لاختراق الجهاز أو عدم التعامل الصحيح مع بعض المدخلات أو غيرها. هذه الأخطاء البرمجية لا يمكن تفاديها, و مهما قمنا بدراسة البرمجيات لتطبيق معين لمحاولة إزالة الأخطاء البرمجية فما يزال هناك مجال للأخطاء “الغير المتوقعة”. فالسؤال الآن هو إن كانت هناك طريقة لتفادي المشاكل المترتبة عن الأخطاء البرمجية بدون الإعتماد على المهمة المستحيلة و هي إزالة جميع الأخطاء.
بشكل آخر, ما نريده هو حل للمشاكل البرمجية التي لا نعرفها. قد يبدو ذلك مستحيلا, و لكن أحد الملاحظات عن الأخطاء البرمجية هي أن الخطأ البرمجي قد لا يتكرر في أكثر من تنفيذ (implementation) مختلف للبرنامج. على سبيل المثال إن طلبت من شخصين مختلفين برمجة نفس التطبيق فإن نسخة المبرمج الأول ستحتوي على أخطاء مختلفة عن الأخطاء في نسخة المبرمج الثاني. هذه الملاحظة هي الطريق الأول لحل مشكلة الأخطاء الغير متوقعة في البرمجيات. فبدلا من تنفيذ برنامج واحد للتطبيق, يمكن عمل أكثر من نسخة عن طريق فرق برمجية مختلفة, و هو ما يسمى البرمجة بنسخ مختلفة (N-version programming).
هل البرمجة بنسخ مختلفة كافية؟ إن أردنا استخدامها لتطبيق معين, قد نقوم بعمل عدة نسخ من البرنامج بحيث إن واجهت أحد النسخ مشكلة غير متوقعة, فإن النسخ الأخرى ستقوم بتصحيحها. لكن ذلك يدفعنا لمشكلة أخرى و هي كيف يمكن للنسخ معرفة أي منهم التي تواجه مشكلة غير متوقعة و أي منهم التي تعمل بشكل صحيح؟ هذه المشكلة تصبح معقدة بشكل أكبر بسبب أن الأخطاء غير متوقعة و قد تكون معقدة بشكل كافي أو بسبب طرف خارجي يؤدي للخطأ الغير متوقع بأن يقنع باقي النسخ بأن التصرف الخاطئ هو الصحيح.
لمواجهة هذه المشكلة, على النسخ المختلفة أن تتوصل للتصرف الصحيح عن طريق العمل سوية و لكن من دون ثقة كاملة في النسخ الأخرى. لنمذجة عدم الثقة بين النسخ المختلفة, فإن كل نسخة تعتبر أن أي نسخة أخرى قد تكون “كاذبة”. الكذب في هذه الحالة قد يكون بسبب خطأ غير متوقع أو اختراق خارجي لأحد النسخ. و تصبح المشكلة الآن هي كيف يمكن لعدة نسخ من التطبيق أن تتوصل لنتيجة واحدة حتى لو كان يوجد حواسيب كاذبة بينهم.
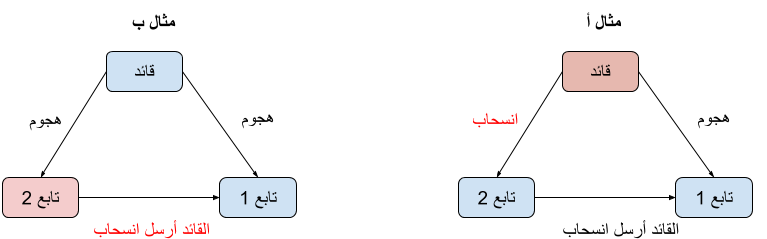
هذه النمذجة لمشكلة التوصل لنتيجة واحدة مع امكانية وجود حواسيب كاذبة هي أحد المشاكل الأساسية في مجال النظم الموزعة. أحد أول الأعمال لحل هذه المشكلة هي ورقة علمية من العام 1982 لليسلي لامبورت, الحائز على جائزة تورينق, و آخرين (1). في تلك الورقة, تم تقديم المشكلة بمثال عن عدة جنرالات بيزنطيين يريدون الهجوم على مدينة! بالتحديد, يوجد 3 جنرالات, أحدهم قائد و الآخرين تابعين. هؤلاء الجنرالات يقفون مع جيوشهم على أطراف مختلفة من المدينة و يريدون الإتفاق إما على الهجوم أو الانسحاب.
(اللون الأحمر في الأمثلة يدل على الطرف الكاذب أو الرسائل الكاذبة)
القائد يفترض أن يقوم بإرسال أمر الهجوم. لكن لنفترض أن أحد الجنرالات الثلاثة كاذب و لنأخذ وجهة نظر أحد التابعَين و لنسمه تابع 1. تابع 1 قد يستقبل أمر “هجوم” من القائد. و لكن ليتأكد من أن القائد لم يقم بالكذب, فإن تابع 1 يسأل تابع 2 عن الأمر الذي تلقاه هو من القائد. قد يرسل تابع 2 أن الأمر الذي تلقاه من القائد هو الانسحاب. في هذه الحالة تابع 1 تلقى أمر هجوم من القائد لكن تابع 2 يقول أنه تلقى أمر انسحاب من القائد. من يصدق تابع 1؟ في هذه الحالة, لا يمكن لتابع 1 معرفة إن كان القائد كاذبا (و قام بارسال رسالتين مختلفتين لتابع 1 و 2 كما في مثال أ بالأعلى) أو إن كان تابع 2 كاذبا (و قام بإرسال رسالة كاذبة لتابع 1 كما في مثال ب بالأعلى).
تلقت مشكلة التوصل لنتيجة واحدة مع امكانية وجود حواسيب كاذبة الكثير من الاهتمام و أصبحت تسمى بمشكلة الجنرالات البيزنطيين, أو مشكلة تخطي الأخطاء البيزنطية. أصبحت هناك العديد من الحلول لهذه المشكلة بطرق مختلفة. قد يكون أكثرها شهرة حاليا هو سلسلة الكتل (blockchain), الحل المستخدم في العملات الإلكترونية. إن أحد أهم المشاكل التي حلتها سلسلة الكتل هي إمكانية القيام بعمليات مالية حتى بوجود حواسيب أو أشخاص كاذبيبن في شبكة العملة الالكترونية.
عن طريق التوصل لحلول لتخطي الأخطاء البيزنطية مع البرمجة بنسخ مختلفة, قد يمكننا تخطي الأخطاء الغير متوقعة في البرمجيات و التي أدت للمشاكل التي استعرضناها في الجزء الأول من التدوينة. لكن, هناك العديد من التحديات اللازم حلها لجعل هذا الطريق ممكنا بشكل أوسع و أكفأ لتغطية مجال أكبر من الأخطاء الغير متوقعة و الحواسيب الكاذبة. هل تعتقد أن هذه التحديات يمكن تخطيها؟